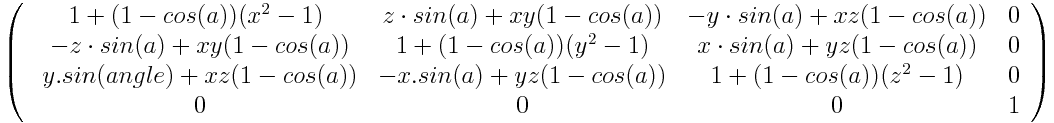rotate3d()

La fonction rotate3d() définit une transformation qui déplace un élément autour d'un axe sans le déformer. L'angle de la rotation est un argument de la fonction. Si l'angle indiqué est positif, le mouvement sera appliqué dans le sens horaire et sinon il sera appliqué dans le sens inverse des aiguilles d'une montre.

Dans l'espace (en trois dimensions), les rotations ont trois degrés de liberté qui définissent l'axe de rotation. Cet axe est défini par un vecteur [x, y, z] et passe par l'origine du repère (définie grâce à la propriété transform-origin). Si le vecteur n'est pas normalisée (autrement si la somme des carrés de ses trois composantes ne vaut pas 1), il sera normalisé par le moteur. Un vecteur qui ne peut être normalisé (par exemple le vecteur nul [0, 0, 0]) empêchera la rotation d'être appliqué mais la propriété CSS restera valide.

Syntaxe

rotate3d(x, y, z, a)

Valeurs

x

Une valeur de type <number> qui définit la composante en X (l'abscisse) du vecteur qui sera l'axe de la rotation.

y

Une valeur de type <number> qui définit la composante en Y (l'ordonnée) du vecteur qui sera l'axe de la rotation.

z

Une valeur de type <number> qui définit la composante en Z (la côte) du vecteur qui sera l'axe de la rotation.

a

Une valeur de type <angle> qui représente l'angle de la rotation. Un angle positif indique une rotation appliquée dans le sens horaire, un angle négatif applique une rotation dans le sens anti-horaire.

Coordonnées cartésiennes sur ℝ2	Coordonnées homogènes sur ℝℙ2	Coordonnées cartésiennes sur ℝ3	Coordonnées homogènes sur ℝℙ3
Cette transformation s'applique dans l'espace (3D) et ne peut pas être représentée en deux dimensions.		$\left(\begin{array}{ccc}1+(1-cos(a))(x^2-1)& z·sin(a)+xy(1-cos(a))& -y·sin(a)+xz·(1-cos(a))\\ -z·sin(a)+xy·(1-cos(a))& 1+(1-cos(a))(y2-1)& x·sin(a)+yz·(1-cos(a))& ysin(a)\; +\; xz(1-cos(a))& -xsin(a)+yz(1-cos(a))& 1+(1-cos(a))(z2-1)& t\\ 0& 0& 0& 1\end{array}\right)$

Exemples

Définir une rotation sur l'axe X

HTML

<p>toto</p>
<p class="transformation">truc</p>

CSS

p { 
  width: 50px;
  height: 50px;
  background-color: teal;
}

.transformation{
  transform: rotate3d(1,0,0,60deg);
  background-color: blue;
}

Résultat

Définir une rotation sur un axe quelconque

HTML

<p>toto</p>
<p class="transformation">truc</p>

CSS

p { 
  width: 50px;
  height: 50px;
  background-color: teal;
}

.transformation {
  transform: rotate3d(1, 2, -1, 192deg);
  background-color: blue;
}

Résultat