Le type de donnée <timing-function> représente une fonction mathématique qui décrit la vitesse à laquelle évolue une valeur unidimensionnelle lors d'une transition ou d'une animation. Cela permet de définir une courbe d'accélération afin que la vitesse de l'animation puisse changer lors de son exécution. Ces fonctions sont souvent appelées « fonction de temporisation » ou « easing functions » (en anglais).
Cette fonction prend comme entrée un ratio de temps (0 : l'état initial, 1 : l'état final) et produit un ratio d'évolution (sous la forme d'une valeur <number>) allant également de 0.0 à 1.0.
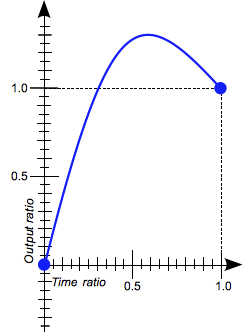
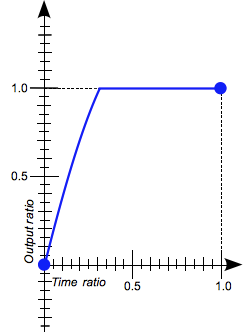
Le ratio de sortie peut être supérieur à 1.0 ou inférieur à 0.0. Cela entraînera l'animation « plus loin » que l'état final ou initial avant de revenir. Cela permettra de créer un effet de rebondissement.
Toutefois, si la valeur de sortie correspondante est entrainée hors de son domaine de validité (par exemple une composante de couleur entraînée au-delà de 255), la valeur est ramenée à la valeur autorisée la plus proche (dans l'exemple : 255).
Valeurs
CSS prend en charge deux types de fonctions de temporisation :
- un sous-ensemble des courbes de Bézier cubiques
- des fonctions en escalier.
Les plus utiles de ces fonctions sont également disponibles via un mot-clé qui permet de les décrire.
La classe de fonctions cubic-bezier()
 |
La notation fonctionnelle Une courbe de Bézier cubique se définit par quatre points P0, P1, P2, et P3. P0 et P3 correspondent respectivement au début et à la fin de la courbe. En CSS, ces points sont fixes car les coordonnées des points expriment des ratios. P0 est donc Tous les courbes de Bézier cubiques ne peuvent pas être utilisées comme des fonctions de temporisation. Certaines de ces courbes ne sont pas des fonctions mathématiques (c'est-à-dire des courbes qui n'ont qu'une valeur pour une abscisse donnée). P0 et P3 sont fixés par la définition CSS et une courbe de Bézier cubique est donc uniquement valide si et seulement si les abscisses des points P1 et P2 sont toutes les deux comprises dans l'intervalle Les courbes de Bézier cubiques pour lesquelles les ordonnées de P1 et/ou P2 sont situées en dehors de l'intervalle Lorsqu'on définit une courbe de Bézier invalide en CSS via |
Syntaxe
cubic-bezier(x1, y1, x2, y2)
avec
- x1, y1, x2, y2
- qui sont des valeurs de type
<number>représentant les abscisses et les ordonnées des points P1 et P2 définissant la courbe de Bézier cubique. x1 et x2 doivent appartenir à l'intervalle [0, 1], sinon la valeur est considérée comme invalide.
Exemples
Voici des courbes de Bézier cubiques qui peuvent être utilisées en CSS :
cubic-bezier(0.1, 0.7, 1.0, 0.1) cubic-bezier(0, 0, 1, 1) /* Des valeurs négatives pour les ordonnées pour */ /* créer du rebondissement */ cubic-bezier(0.1, -0.6, 0.2, 0) /* Idem avec des valeurs > 1 */ cubic-bezier(0, 1.1, 0.8, 4)
En revanche, ces définitions sont invalides :
/* Though the animated output type may be a color, Bézier curves work w/ numerical ratios.*/ cubic-bezier(0.1, red, 1.0, green) /* Abscissas must be in the [0, 1] range or the curve is not a function of time. */ cubic-bezier(2.45, 0.6, 4, 0.1) /* The two points must be defined, there is no default value. */ cubic-bezier(0.3, 2.1) /* Abscissas must be in the [0, 1] range or the curve is not a function of time. */ cubic-bezier(-1.9, 0.3, -0.2, 2.1)
La classe de fonction steps()
.png) |
.png) |
La notation fonctionnelle |
steps(2, start) |
steps(4, end) |
Syntaxe
steps(nombre_de_marche, direction)
avec
nombre_de_marche- Un entier (valeur de type
<integer>qui représente le nombre de marches composant la fonction en escalier. direction- Un mot-clé qui indique si la fonction est continue à gauche ou continue à droite :
startindique une fonction continue à gauche : la première marche se déroule à partir du début de l'animationendindique une fonction continue à gauche : la dernière marche se déroule lors de la fin de l'animation.
endest la valeur par défaut..
Exemples
Voici des exemples de fonction de temporisation en escalier valides :
/* Il y a cinq marches et la dernière est utilisée */ /* avant la fin de l'animation. */ steps(5, end) /* Une fonction à deux marches dont la première se */ /* déroule au début de l'animation. */ steps(2, start) /* Le deuxième paramètre est facultatif. */ steps(2)
En revanche, celles-ci sont invalides :
/* Le premier paramètre doit être un entier (type */ /* <integer>) */ steps(2.0, end) /* Le nombre d'étapes ne peut pas être négatif. */ steps(-3, start) /* Il ne peut pas être nul.*/ steps(0, end)
Mots-clés pour les fonctions de temporisation usuelles
linear
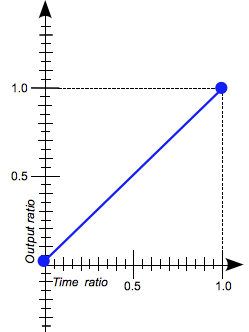 |
Ce mot-clé représente la fonction de temporisation cubic-bezier(0.0, 0.0, 1.0, 1.0). Cette fonction permet de passer de l'état initial à l'état final avec une vitesse constante. |
ease
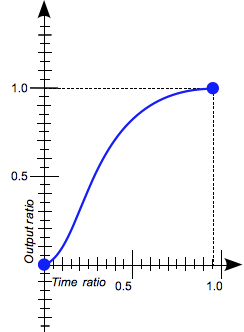 |
Ce mot-clé représente la fonction de temporisation cubic-bezier(0.25, 0.1, 0.25, 1.0). Cette fonction est semblable à ease-in-out sauf qu'elle accélère plus rapidement au début et ralentit dès la moitié du parcours.. |
ease-in
 |
Ce mot-clé représente la fonction de temporisation cubic-bezier(0.42, 0.0, 1.0, 1.0). L'animation démarre lentement puis accélère progressivement jusqu'à atteindre l'état final. Cela donne l'impression que l'animation s'arrête brutalement. |
ease-in-out
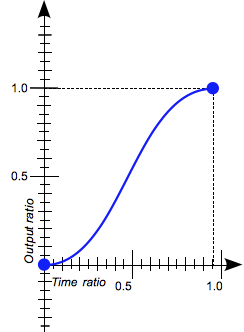 |
Ce mot-clé représente la fonction de temporisation cubic-bezier(0.42, 0.0, 0.58, 1.0). L'animation démarre lentement puis accélère progressivement avant de ralentir à nouveau à l'approche de l'état final. Dans la première phase, la courbe se comporte comme ease-in et dans la deuxième moitié, elle se comporte comme ease-out. |
ease-out
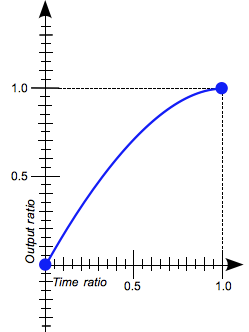 |
Ce mot-clé représente la fonction de temporisation cubic-bezier(0.0, 0.0, 0.58, 1.0). L'animation démarre rapidement puis ralentit progressivement avant d'atteindre son état final. |
step-start
.png) Ce mot-clé représente la fonction de temporisation Ce mot-clé représente la fonction de temporisation steps(1, start). Avec cette fonction, l'animation passe directement à l'état final dès le début et conserve cet état jusqu'à la fin de l'animation. |
step-end
.png) |
Ce mot-clé représente la fonction de temporisation steps(1, end). Avec cette fonction, l'animation reste dans son état initial tout le long de la durée et passe directement à la position finale à la toute fin. |
Spécifications
| Spécification | État | Commentaires |
|---|---|---|
| CSS Transitions La définition de '<timing-function>' dans cette spécification. |
Version de travail | Définition implicite du type. |
| CSS Animations La définition de '<timing-function>' dans cette spécification. |
Version de travail | Définition implicite du type avec une référence vers la définition du module CSS pour les transitions. |
Compatibilité des navigateurs
| Fonctionnalité | Firefox (Gecko) | Chrome | Internet Explorer | Opera | Safari |
|---|---|---|---|---|---|
| Support simple | 4.0 (2.0) | 4.0 | 10 | 10.5 | 3.1 |
cubic-bezier() avec une ordonnée en dehors de [0,1] |
4.0 (2.0) | 16.0 | 10 | 12.1 | Nightly |
steps() |
4.0 (2.0) | 8.0 | 10 | 12.1 | 5.1 |
| Fonctionnalité | Firefox Mobile (Gecko) | Android | IE Phone | Opera Mobile | Safari Mobile |
|---|---|---|---|---|---|
| Support simple | 4.0 (2.0) | 4.0 | Pas de support | 10 | 2.0 |
cubic-bezier() avec une ordonnée en dehors de [0,1] |
4.0 (2.0) | (Oui) | Pas de support | Pas de support | Pas de support |
steps() |
4.0 (2.0) | 4.0 | Pas de support | Pas de support | 5.0 |
Voir aussi
- Les propriétés
transition-timing-functionetanimation-timing-functionqui utilisent une valeur de type<timing-function> - La référence CSS